בפרקים הקודמים עסקנו במערכים חד-מימדיים, המאפשרים שמירה של רצף נתונים תחת שם אחד. עם זאת, קיימים מבני נתונים מורכבים יותר הדורשים ייצוג של טבלה. מערך דו-מימדי הוא מבנה נתונים המורכב משורות ועמודות, בדומה לטבלה.
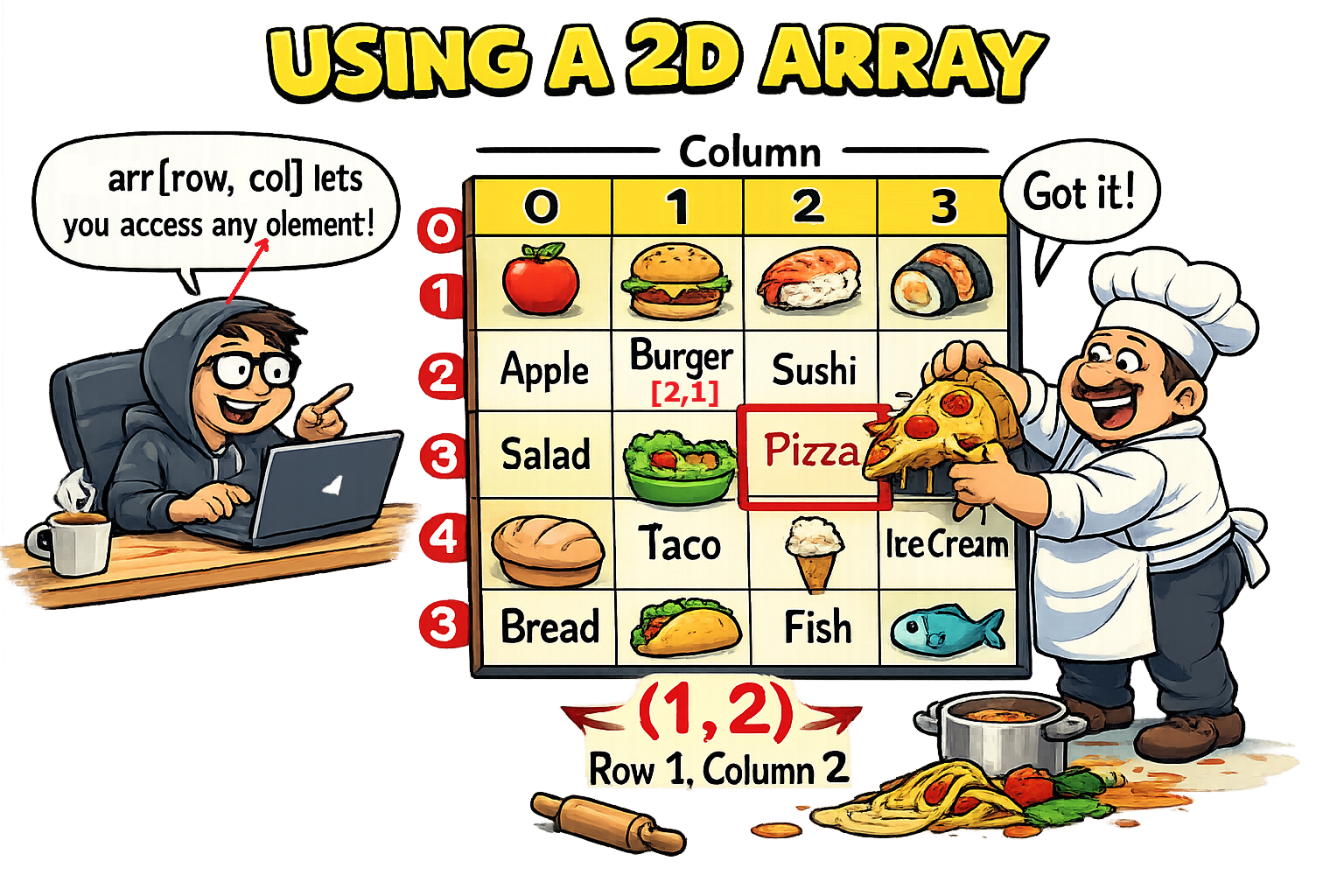
סדר הוראה: אני מעדיף ללמד לאחר מספר שיעורים של עצמים כספירלה על מערכים ולולאות.
מבוא למערך דו-מימדי (מטריצה)
דוגמה קלאסית להמחשת המושג היא תבנית ביצים, שבה הביצים מסודרות בשתי שורות ומספר עמודות.

כאשר אנו מדברים על מערך דו-מימדי, אנו למעשה מדברים על אוסף של איברים מאותו הטיפוס, כאשר לכל המערך יש שם מזהה אחד. מערך זה נקרא לעיתים קרובות גם מטריצה (Matrix).
במערך דו-מימדי יש מספר שורות ומספר עמודות במבנה של טבלה, כאשר כל תא בטבלה מזוהה על ידי זוג אינדקסים: אינדקס השורה ואינדקס העמודה.
שימושים בחיי היומיום ובמחשב
המערך הדו-מימדי נפוץ מאוד ביישומי תוכנה רבים המייצגים מידע טבלאי. לדוגמה, נתוני מזג אוויר הנאספים לאורך שנים מוצגים לרוב בטבלה שבה השורות מייצגות פרמטרים שונים (טמפרטורה ממוצעת, משקעים, לחות) והעמודות מייצגות את חודשי השנה.
| Parameter | Jan | Feb | Mar | Apr | May | Jun |
|---|---|---|---|---|---|---|
| Avg Temp | 69 | 73 | 75 | 73 | 69 | 66 |
| High Temp | 75 | 80 | 82 | 80 | 77 | 73 |
| Precipitation | 53.2 | 9.5 | 8.0 | 5.6 | 2.3 | 1.7 |
שימוש נפוץ נוסף הוא במשחקי לוח. משחקים כמו “איקס-עיגול” (Tic-Tac-Toe), “ארבע בשורה” (Connect Four), שחמט או דמקה מבוססים כולם על רשת (Grid) של משבצות המסודרות בשורות ועמודות.
תרגול אינטראקטיבי ראשוני (קל) למערך דו-מימדי
פנייה לאיבר במערך דו-מימדי
בניגוד למערך חד-מימדי שבו השתמשנו באינדקס אחד בלבד, פנייה לאיבר במערך דו-מימדי נעשית בעזרת שני אינדקסים: אינדקס השורה ואינדקס העמודה.
הכללים הבסיסיים לפנייה לאיבר הם:
- האינדקסים חייבים להיות מטיפוס שלם (int).
- במערך בעל \(N\) שורות ו-\(M\) עמודות:
- אינדקסי השורות הם בטווח שבין \(0\) ל- \(N-1\).
- אינדקסי העמודות הם בטווח שבין \(0\) ל- \(M-1\).
כדי לפנות לאיבר, נכתוב את שם המערך ולאחריו בסוגריים מרובעים את אינדקס השורה ואינדקס העמודה מופרדים בפסיק: [row, col].
לדוגמה, אם נתונה המטריצה mat הבאה בגודל 3 שורות על 4 עמודות:
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 2 | 9 | 4 | 2 |
| 1 | 7 | 4 | 3 | 5 |
| 2 | 6 | 1 | 8 | 1 |
הקוד Console.WriteLine(mat[1,3]); ידפיס את הערך 5, מכיוון שהוא נמצא בשורה באינדקס 1 ובעמודה באינדקס 3.
==פנייה לאינדקס שחורג מגבולות המערך== (למשל פנייה לשורה 3 במערך שיש בו רק 3 שורות, כלומר האינדקס המקסימלי הוא 2) תגרום לשגיאת זמן ריצה (Exception) מסוג IndexOutOfRangeException.
דוגמאות לניהול נתונים במטריצות
דוגמה 1: מספר תלמידים בבית ספר
נניח שבבית ספר תיכון יש 3 שכבות (י’, י”א, י”ב) ובכל שכבה יש 7 כיתות. ניתן לייצג את מספר התלמידים בכל כיתה באמצעות מטריצה שבה השורות הן השכבות והעמודות הן הכיתות.
| שכבה / כיתה | כיתה 1 | כיתה 2 | כיתה 3 | כיתה 4 | כיתה 5 | כיתה 6 | כיתה 7 | English |
|---|---|---|---|---|---|---|---|---|
| שכבת י’ | 40 | 45 | 38 | 33 | 33 | 38 | 36 | Grade 10 |
| שכבת י”א | 42 | 40 | 40 | 38 | 41 | 39 | 36 | Grade 11 |
| שכבת י”ב | 33 | 38 | 44 | 35 | 40 | 39 | 34 | Grade 12 |
מהטבלה הזו ניתן להפיק נתונים רבים, כגון מספר התלמידים בכל שכבה (סכום שורה), מספר התלמידים בכל בית הספר (סכום כל התאים) או זיהוי הכיתה הגדולה ביותר.
דוגמה 2: ציוני בגרות ארציים
ניתן להשתמש במטריצה כדי להציג ממוצעי ציונים במקצועות שונים בערים שונות.
| עיר / מקצוע | מתמטיקה | אנגלית | תנ”ך |
|---|---|---|---|
| תל אביב | 78 | 83 | 75 |
| ירושלים | 80 | 80 | 88 |
| חיפה | 85 | 77 | 80 |
| ראשון לציון | 79 | 75 | 90 |
| חולון | 81 | 83 | 78 |
חישובים לדוגמה על בסיס המטריצה (נניח ששמה mat):
- חישוב ממוצע המבחנים בחיפה (שורה באינדקס 2):
(mat[2,0] + mat[2,1] + mat[2,2]) / 3.0. - חישוב הממוצע הארצי במתמטיקה (עמודה באינדקס 0):
(mat[0,0] + mat[1,0] + mat[2,0] + mat[3,0] + mat[4,0]) / 5.0.
הגדרה ובנייה של מערך דו-מימדי ב-C#
כמו במערך חד-מימדי, קיימות שתי דרכים עיקריות להגדיר ולבנות מערך דו-מימדי.
דרך א’: הגדרה ובנייה בשורה אחת
המבנה הכללי הוא:
elementType[,] arrayName = new elementType[rowCount, columnCount];
// לדוגמא:
int[,] mat = new int[3, 5];
דוגמאות. חשוב להשתמש בלשון רבים:
// מערך גבהים בגודל 10 שורות ו-3 עמודות מטיפוס ממשי
double[,] heights = new double[10, 3];
// מערך תווים בגודל 8 על 8 (לוח משחק)
char[,] signs = new char[8, 8];
// מערך ציונים ל-35 תלמידים ב-5 מקצועות
int[,] marks = new int[35, 5];
// מערך מכוניות בחניון עם 5 שורות של 35 מכוניות
Car[,] cars = new Car[5, 55]; // (וגם בזה לא היינו משתמשים במציאות) parking ולא
המקבילה בשפת Java
// 10 rows, 3 columns
double[][] heights = new double[10][3]; // זה מערך של מערכים בעוד [,] הוא בלוק רציף אחד
// 8x8 grid
char[][] signs = new char[8][8];
// 35 students, 5 subjects
int[][] marks = new int[35][5];
דרך ב’: הגדרה ובנייה בשורות נפרדות
לעיתים נרצה להצהיר על המערך בראש התוכנית ורק מאוחר יותר להקצות לו זיכרון (למשל לאחר שקיבלנו את הגודל מהמשתמש).
double[,] heights; // הצהרה
heights = new double[10, 3]; // בנייה והקצאת זיכרון
המקבילה בשפת Java
double[][] heights; // declaration
heights = new double[10][3]; // allocation
בניית המערך יכולה להתבצע בכל מקום בקוד, וגודלו יכול להיקבע גם באמצעות משתנים ולא רק על ידי קבועים מספריים.
אתחול ידני של מטריצה
ניתן לאתחל מטריצה כבר בשלב ההגדרה בעזרת סוגריים מסולסלים, בדומה למערך חד-מימדי. במקרה זה, כל שורה מיוצגת על ידי תת-אוסף של סוגריים מסולסלים.
// אתחול מטריצת מספרים שלמים 3x4
int[,] arrInt2D = new int[,] {
{ 29, 43, 21, 26 },
{ 77, 87, 81, 80 },
{ 92, 93, 97, 91 }
};
// אתחול מטריצת תווים 3x4
char[,] arrChar2D = new char[,] {
{ 'X', 'O', 'X', 'O' },
{ '~', '~', '~', '~' },
{ 'A', 'B', 'C', 'D' }
};
המקבילה בשפת Java
// 3x4 int matrix
int[][] arrInt2D = new int[][] {
{ 29, 43, 21, 26 },
{ 77, 87, 81, 80 },
{ 92, 93, 97, 91 }
};
// 3x4 char matrix
char[][] arrChar2D = new char[][] {
{ 'X', 'O', 'X', 'O' },
{ '~', '~', '~', '~' },
{ 'A', 'B', 'C', 'D' }
};
פעולות בסיסיות על מטריצות
כדי לעבוד עם מטריצות בצורה יעילה, עלינו להכיר את הפעולות הבסיסיות של קלט, פלט ושימוש בפונקציות עזר.
פונקציית GetLength
במערך חד-מימדי השתמשנו בתכונה Length כדי לקבל את מספר האיברים. במערך דו-מימדי, Length יחזיר את סך כל האיברים (שורות כפול עמודות).
כדי לקבל את הגודל של מימד ספציפי, נשתמש בפעולה GetLength(dim):
mat.GetLength(0)- מחזיר את מספר השורות.mat.GetLength(1)- מחזיר את מספר העמודות.
קלט למערך דו-מימדי
קליטת נתונים למערך שלם מתבצעת בדרך כלל באמצעות לולאות מקננות (Nested Loops).
const int ROW = 5, COL = 4;
int[,] mat = new int[ROW, COL];
// לולאה לקליטת נתונים לפי סדר השורות (שורה ראשונה, אז שנייה וכו')
for (int i = 0; i < ROW; i++)
{
for (int j = 0; j < COL; j++)
{
Console.Write($"Enter value for [{i},{j}]: ");
mat[i, j] = int.Parse(Console.ReadLine());
}
}
המקבילה בשפת Java
final int LINE = 5, COL = 4;
int[][] mat = new int[LINE][COL];
Scanner scanner = new Scanner(System.in);
for (int i = 0; i < LINE; i++)
{
for (int j = 0; j < COL; j++)
{
System.out.print("Enter value for [" + i + "," + j + "]: ");
mat[i][j] = Integer.parseInt(scanner.nextLine());
}
}
ניתן גם לקלוט נתונים לפי סדר העמודות על ידי החלפת סדר הלולאות (הלולאה החיצונית תרוץ על העמודות והפנימית על השורות).
פלט של מערך דו-מימדי
כדי להדפיס את המערך בצורת טבלה, נשתמש בלולאות מקננות ונדאג לרדת שורה לאחר סיום הדפסת כל שורת נתונים.
for (int i = 0; i < mat.GetLength(0); i++)
{
for (int j = 0; j < mat.GetLength(1); j++)
{
Console.Write(mat[i, j] + " ");
}
Console.WriteLine(); // ירידת שורה בסיום כל שורת נתונים
}
המקבילה בשפת Java
for (int i = 0; i < mat.length; i++)
{
for (int j = 0; j < mat[i].length; j++)
{
System.out.print(mat[i][j] + " ");
}
System.out.println(); // end of row
}
השמה ושינוי ערכים
כל איבר במטריצה מתנהג כמשתנה רגיל מהטיפוס שהוגדר. ניתן לבצע עליו פעולות חשבוניות, השמה של מספרים אקראיים ועוד.
public static Random rnd = new Random(); // ניגע בזה שוב בהמשך
public static void Main()
{
num = mat[i, j]; // השמת ערך מהמטריצה למשתנה
mat[i, j]++; // הגדלת ערך של תא ספציפי ב-1
mat[i, j] = rnd.Next(1, 31); // השמת מספר אקראי בין 1 ל-30
}
המקבילה בשפת + התייחסות ל-static Random Java
קישור להסבר מפורט לגבי הצורך באיתחול סטטי של Random
public static Random rnd = new Random();
public static void main()
{
num = mat[i][j]; // read element
mat[i][j]++; // increment by 1
mat[i][j] = rnd.nextInt(30) + 1; // 1..30
}
תרגול כיתה: הבנת לולאות על מטריצה
נתונה מטריצה ריבועית m בגודל 5x5 המכילה את המספרים 1 עד 25 לפי הסדר:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 6 | 7 | 8 | 9 | 10 |
| 2 | 11 | 12 | 13 | 14 | 15 |
| 3 | 16 | 17 | 18 | 19 | 20 |
| 4 | 21 | 22 | 23 | 24 | 25 |
נבחן מה ידפיסו קטעי הקוד הבאים:
for(i=0; i<5; i++) Console.Write(m[2,i]);-> ידפיס את כל שורה 2: 11, 12, 13, 14, 15.for(i=0; i<5; i++) Console.Write(m[i,2]);-> ידפיס את כל עמודה 2: 3, 8, 13, 18, 23.Console.Write(m);-> ידפיס את שם הטיפוס (System.Int32[,])Console.Write(m[0,5]);-> ==שגיאה!== אינדקס מחוץ לטווח (האינדקס המקסימלי הוא 4).for(i=0; i<5; i++) Console.Write(m[i,i]);-> ידפיס את האלכסון הראשי: 1, 7, 13, 19, 25.
תרגול אינטראקטיבי נוסף: לולאות במערך דו-מימדי
מטריצה ריבועית ואלכסונים
מטריצה נקראת מטריצה ריבועית כאשר מספר השורות שלה שווה למספר העמודות \(N = M\). במטריצה ריבועית קיימים שני מושגים חשובים: אלכסון ראשי ואלכסון משני.
האלכסון הראשי
האלכסון הראשי עובר מהפינה השמאלית העליונה לפינה הימנית התחתונה. ==החוקיות באלכסון הראשי:== אינדקס השורה שווה לאינדקס העמודה (\(i == j\)).
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0,0 | 0,1 | 0,2 |
| 1 | 1,0 | 1,1 | 1,2 |
| 2 | 2,0 | 2,1 | 2,2 |
האלכסון המשני
האלכסון המשני עובר מהפינה הימנית העליונה לפינה השמאלית התחתונה. ==החוקיות באלכסון המשני:== סכום האינדקסים (שורה + עמודה) הוא קבוע ושווה ל-\(N-1\).
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0,0 | 0,1 | 0,2 |
| 1 | 1,0 | 1,1 | 1,2 |
| 2 | 2,0 | 2,1 | 2,2 |
שימו לב שבאלכסון המשני, ככל שאינדקס השורה גדל, אינדקס העמודה קטן בהתאמה כדי לשמור על סכום קבוע.
סיכום והשוואה למערך חד-מימדי
לסיכום הנושא, נשווה בין המאפיינים של מערך חד-מימדי למערך דו-מימדי:
| מאפיין | מערך חד-מימדי | מערך דו-מימדי (מטריצה) | English |
|---|---|---|---|
| כמות אינדקסים | 1 | 2 (שורה, עמודה) | Dimensions |
| גישה לאיבר | arr[i] |
mat[i, j] |
Access |
| קבלת גודל | arr.Length |
mat.GetLength(0/1) |
Size / Length |
| לולאות לעיבוד | לולאת for אחת |
לולאות מקננות (Nested) | Loops |
| מבנה בזיכרון | רצף ליניארי | טבלה / רשת | Structure |
כדי להבין את המטריצה בצורה הטובה ביותר, ניתן לדמות אותה לבניין מגורים: הקומות הן השורות, ומספרי הדירות בכל קומה הם העמודות. כדי להגיע לדירה מסוימת (איבר), עלינו לדעת גם באיזו קומה היא נמצאת וגם מהו מספרה באותה קומה.
חומר למחיקה - נא להתעלם
| סוג | הגדרה | תיאור |
|---|---|---|
| תכונות | string nafasdfme | שם הדלי |
| סתם טקסט ארוך | int capacity | קיבולת הדלי |
טעימה לסיום: משחק החיים (Game of Life)
הערה: שאלה יחסית קשה המתאימה לתלמידים שלומדים מערך דו-ממדי בסוף החומר וכבר שולטים בחומר.
משחק החיים הוא משחק סימולציה המתאר את מחזור החיים של יצורים (או תאים) חיים. הסימולציה מתרחשת במטריצה שבה כל תא מייצג אתר מחיה - בכל אתר אחד משני מצבים: I. “יש חיים” - אתר מאוכלס ביצור - מסומן באמצעות המספר 1. II. “אין חיים” - אתר ריק - מסומן באמצעות המספר 0.
חוקי הגנטיקה במשחק החיים:
- כל יצור שיש לו פחות משני שכנים, מת מבדידות.
- כל יצור שיש לו שניים או שלושה שכנים, ממשיך לחיות לדור הבא.
- כל יצור שיש לו יותר משלושה שכנים, מת מצפיפות.
- כל אתר ריק שיש לו בדיוק שלושה שכנים, קם לתחייה (נולד בו יצור).
מידע נוסף בוויקיפדיה: Conway’s Game of Life
Glider

Blinker

Toad

להמשך תרגול כנסו למערכת ההגשות בכיתה שלכם.